Maximum Height Calculator – Projectile Motion

Maximum height in projectile motion

Use this maximum height calculator to figure out what is the maximum vertical position of an object in projectile motion.

Last updated: December 29, 2025

CreatorFrank Zhao

Velocity

More info

m/s

Angle of launch

More info

deg

Initial height

More info

Horizontal velocity

More info

m/s

Vertical velocity

More info

m/s

Maximum height

More info

1Horizontal velocity component

v_x = v \cos(\alpha)

2Vertical velocity component

v_y = v \sin(\alpha)

3Maximum height

h_{\max} = h_0 + \frac{v_y^2}{2g} = h_0 + \frac{v^2 \sin^2(\alpha)}{2g}

v

Velocity

v_x

Horizontal velocity

v_y

Vertical velocity

\alpha

Angle of launch

h_0

Initial height

h_{\max}

Maximum height

Introduction / Overview

The Maximum Height Calculator is a tool for finding the highest vertical position a launched object reaches during projectile motion. Whether you throw a ball, kick a soccer shot, or run a classroom experiment, it helps you answer one simple question: “How high will it go?”

What problems does it solve?

It quickly links your inputs (launch speed, angle, and initial height) to peak height. It can also work in reverse: if you know the peak height, it can help you back-calculate other values.

Who is this for?

Students checking homework, athletes and coaches sanity-checking a throw, makers building launchers, and anyone who wants a fast, unit-safe answer.

🧠

Reliability note:

The calculator uses standard constant-acceleration physics with gravity. It assumes no air resistance and a constant gravitational acceleration.

How to find the maximum height of a projectile?

A projectile rises until gravity slows the vertical motion to a stop. At the very top of the trajectory, the vertical velocity is: $v_y = 0$ .

The 3 key ideas (no heavy math):

Split the launch speed into components: $v_{y0} = v_0\sin(\alpha)$ .
Time to the peak happens when $v_y(t) = v_{y0} - g t = 0$ .
Height gained depends on the vertical part only (the horizontal speed doesn’t lift the projectile).

A quick mental shortcut

If you launch at $\alpha = 0^\circ$ (perfectly horizontal), then $v_{y0} = 0$ and the projectile never rises above the launch height. So: $h_{\max} = h_0$ .

Maximum height calculator helps you find the answer

You can use this calculator in a “textbook” direction (give it the launch conditions and read the peak height), or in a “reverse” direction (give it peak height and solve for missing inputs). Either way, it’s designed for quick what-if experiments.

Enter the launch velocity

Type the initial speed and choose units (for example, ft/s or m/s).

Enter the launch angle

Use degrees or radians. The calculator handles conversions. Remember: $\alpha = 90^\circ$ is straight up.

(Optional) Enter initial height

If you launch from a platform, enter the starting height. If you launch from the ground, set it to 0.

Read the maximum height

The maximum height updates instantly. If you change any input, the peak height will follow.

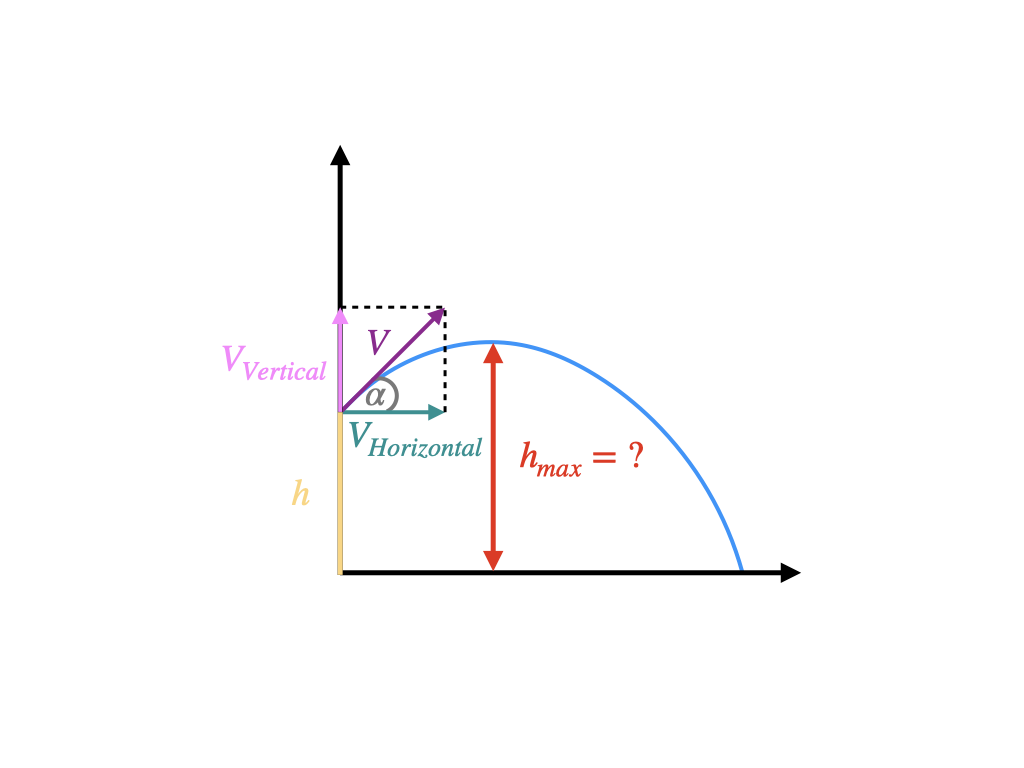
Screenshot / diagram

Projectile motion diagram for maximum height

The diagram is a visual reminder: only the vertical motion determines the peak height.

Example 1: Can a 30 ft/s kick clear a 13 ft fence?

Suppose you kick a ball at $v_0 = 30\ \mathrm{ft/s}$ with an angle of $\alpha = 70^\circ$ from ground level $h_0 = 0\ \mathrm{ft}$ . Ignoring air resistance, the peak height is:

h_{\max} = h_0 + \frac{v_0^2\sin^2(\alpha)}{2g}

=

0 + \frac{30^2\sin^2(70^\circ)}{2\cdot 32.174}

\approx

12.35\ \mathrm{ft}

So it tops out at about 12.35 ft — just under the 13 ft fence. To clear it, you’d need a bit more speed, or a slightly different angle.

Example 2: Launching from a 2 m platform

Now let’s use SI units: $v_0 = 20\ \mathrm{m/s}$ , $\alpha = 45^\circ$ , and $h_0 = 2\ \mathrm{m}$ .

h_{\max}

=

2 + \frac{20^2\sin^2(45^\circ)}{2\cdot 9.80665}

\approx

12.20\ \mathrm{m}

The projectile peaks at about 12.2 m above the ground. Notice how the initial height simply shifts the final answer upward.

Real-World Examples / Use Cases

⚽

Sports (kicks and throws)

Inputs: $v_0 = 25\ \mathrm{m/s},\ \alpha = 55^\circ,\ h_0 = 0$

Result: $h_{\max} \approx 26.0\ \mathrm{m}$

Great for quick “will it clear the bar?” checks.

🏗️

Launching from a platform

Inputs: $v_0 = 18\ \mathrm{m/s},\ \alpha = 40^\circ,\ h_0 = 8\ \mathrm{m}$

Result: $h_{\max} = h_0 + \frac{v_0^2\sin^2\alpha}{2g}$

Useful in labs and simple engineering demos.

🎮

Game development tuning

Inputs: $v_0 \text{ and } \alpha$

Result: $h_{\max}$

Balance “arc height” so jumps feel right.

🎓

Homework sanity checks

Inputs: $v_0,\ \alpha,\ h_0$

Result: $h_{\max} \text{ and } t_h$

Cross-check hand calculations quickly.

🧪

Classroom experiments

Inputs: $h_{\max} \text{ observed}$

Result: $v_{y0} = \sqrt{2g(h_{\max}-h_0)}$

Back-calculate vertical launch speed from data.

Want the full picture (range + time + max height)? Try the Projectile Motion Calculator.

Common Scenarios / When to Use

✅
You know speed and angle
This is the classic setup. Enter $v_0$ and $\alpha$ and read $h_{\max}$ .
✅
You measured peak height
If you can estimate $h_{\max}$ (video analysis, a marked wall, or a sensor), the calculator can help infer vertical launch speed.
✅
You’re studying special angles
For $\alpha = 90^\circ$ the motion is purely vertical. For $\alpha = 0^\circ$ it becomes a horizontal launch.
❌
You’re in strong air resistance
Golf balls, feathers, long-range ballistics, and high-speed projectiles can deviate a lot from the no-drag model. In that case, treat this calculator as a baseline approximation.

Tips & Best Practices

Use realistic angles

Most real throws are somewhere between $20^\circ$ and $70^\circ$ . If you type extreme angles, the calculator is still correct, but the scenario may not match reality.

Sanity-check units

Peak height scales with $v_0^2$ . If your answer looks 10× too big, it’s often a unit mix-up (mph vs m/s, ft vs m).

Remember: only vertical speed lifts

If you keep $v_{y0}$ the same (even if you change the horizontal speed), the peak height stays the same.

Pair with range/time tools

If your next question is “How far?” or “How long?”, jump toRangeorTime of flightcalculators.

Important: this calculator ignores air resistance. If your object is very light or slow (like a shuttlecock), real-life peak height will likely be lower than the idealized estimate.

Calculation Method / Formula Explanation

The maximum height comes from the vertical motion with constant acceleration $-g$ . Start with the vertical velocity equation:

v_y(t) = v_{y0} - g t

Variables (what each symbol means)

$v_0$ : initial speed
$\alpha$ : launch angle
$h_0$ : initial height
$h_{\max}$ : maximum height
$g$ : gravitational acceleration

At the highest point, $v_y = 0$ . Solve for the time to peak:

0 = v_{y0} - g t_h

\Rightarrow

t_h = \frac{v_{y0}}{g} = \frac{v_0\sin(\alpha)}{g}

The vertical displacement equation is:

y(t) = v_{y0} t - \frac{g t^2}{2}

Plug in $t = t_h$ and add the initial height:

h_{\max} = h_0 + v_{y0} t_h - \frac{g t_h^2}{2}

=

h_0 + \frac{v_{y0}^2}{2g}

=

h_0 + \frac{v_0^2\sin^2(\alpha)}{2g}

Special cases (quick intuition)

If $\alpha = 90^\circ$ , then $\sin(\alpha)=1$ and the formula becomes $h_{\max} = h_0 + \frac{v_0^2}{2g}$ .
If $\alpha = 45^\circ$ , then $\sin^2(\alpha)=\frac{1}{2}$ and $h_{\max} = h_0 + \frac{v_0^2}{4g}$ .
If $\alpha = 0^\circ$ , then $h_{\max}=h_0$ (no upward component).

Related Concepts / Background Info

Why max height depends on the vertical part

Projectile motion is two independent motions: a horizontal motion with (approximately) constant speed, and a vertical motion with constant acceleration. The peak height is controlled by $v_{y0}$ and $g$ only.

Mass doesn’t matter (in this model)

With no drag, the equations for height don’t include mass. In real life, mass can matter indirectly because it changes how air resistance affects the object.

🧩

Next step ideas:

Once you have $h_{\max}$ , you may want to compute the full flight path or landing distance. Use the Projectile Range Calculator or the Projectile Motion Calculator.

FAQs

How do I find the maximum height of a ball thrown up?

Use $h_{\max} = h_0 + \frac{v_{y0}^2}{2g}$ where $v_{y0}=v_0\sin(\alpha)$ . If you throw straight up, then $\alpha=90^\circ$ and $v_{y0}=v_0$ .

What angle has the longest flight time (ignoring air resistance)?

For a fixed launch speed, flight time depends on the vertical component, so it’s longest at $\alpha = 90^\circ$ . A common approximation is $t \approx \frac{2v_0\sin(\alpha)}{g}$ when launching and landing at the same height.

Does mass affect maximum height?

In the ideal no-drag model: no. The peak height depends on $v_0$ , $\alpha$ , $h_0$ , and $g$ . With air resistance, different masses and shapes can behave differently.

What factors affect projectile motion in real life?

The big one is aerodynamic drag (air resistance). Wind, spin (Magnus effect), and even changing $g$ slightly with altitude can matter in precise applications.

Why does a higher angle usually increase max height?

Because the vertical component $v_{y0}=v_0\sin(\alpha)$ increases with $\alpha$ (up to $90^\circ$ ), and $h_{\max}-h_0 \propto v_{y0}^2$ .

What if I only know the max height — can I solve for launch speed?

Yes. Rearrange the formula: $v_{y0}=\sqrt{2g(h_{\max}-h_0)}$ . Then use $v_0 = \frac{v_{y0}}{\sin(\alpha)}$ if you also know $\alpha$ .

Why is my measured maximum height lower than the calculator?

Most commonly: air resistance, launch speed overestimated, or the launch angle is not what you think. Small angle errors matter because $\sin^2(\alpha)$ changes quickly at steep angles.

Is this calculator accurate for very long distances or bullets?

Use it as a baseline only. Long-range ballistics require drag models, and sometimes Earth curvature and varying air density.

Limitations / Disclaimers

This calculator uses an ideal projectile model: no air resistance, no wind, and constant gravity. Use it for education, planning, and rough estimates — not as a substitute for professional engineering or safety analysis.

External References / Sources

Calculus: Early Transcendentals (Ninth Edition)
Stewart, James; Clegg, Dan; Watson, Saleem (2021)
ISBN: 978-1-337-61392-7 | p.919
Doing Physics with Scientific Notebook: A Problem Solving Approach
Gallant, Joseph (2012)
ISBN: 978-1-119-94194-1 | p.132
View on Google Books →
Classical Mechanics
Tatum (2019) | Chapter 7
PDF Link →
Classical Dynamics of Particles and Systems
Stephen T. Thornton; Jerry B. Marion (2007)
ISBN: 978-0-495-55610-7 | p.59
View on Google Books →
Classical Mechanics: Point Particles and Relativity
Walter Greiner (2004)
ISBN: 0-387-95586-0 | p.181
View on Google Books →
Two New Sciences
Galileo Galilei (1638) | p.249
Historic original research on projectile motion

Related Calculators

Trajectory Calculator

Have a look at the flight path of the object with this trajectory calculator.

Try Now

Free Fall Calculator

Calculate free fall parameters including gravitational acceleration, drop height, fall duration, and impact velocity. Supports bidirectional LRU solving with unit conversions.

Try Now

Free Fall with Air Resistance Calculator

Calculate free fall with quadratic air drag, including terminal velocity, fall time, maximum velocity, and drag force. Supports air resistance coefficient calculation from object properties.

Try Now

Projectile Range Calculator

Calculate the horizontal range of a projectile based on velocity, angle, and initial height. Supports bidirectional calculation with multiple unit systems.

Try Now

Projectile Motion Calculator

Calculate projectile trajectory parameters including launch velocity, angle, distance, maximum height, and flight time with bidirectional solving.

Try Now

Time of Flight Calculator – Projectile Motion

Check out how long a projectile remains in the air with this time of flight calculator.

Try Now

Maximum Height Calculator – Projectile Motion

Introduction / Overview

What problems does it solve?

Who is this for?

How to find the maximum height of a projectile?

A quick mental shortcut

Other tools related to projectiles' motion

Projectile Motion Calculator

Projectile Range Calculator

Time of Flight Calculator – Projectile Motion

Horizontal Projectile Motion Calculator

Maximum height calculator helps you find the answer

Example 1: Can a 30 ft/s kick clear a 13 ft fence?

Example 2: Launching from a 2 m platform

Real-World Examples / Use Cases

Sports (kicks and throws)

Launching from a platform

Game development tuning

Homework sanity checks

Classroom experiments

Common Scenarios / When to Use

You know speed and angle

You measured peak height

You’re studying special angles

You’re in strong air resistance

Tips & Best Practices

Use realistic angles

Sanity-check units

Remember: only vertical speed lifts

Pair with range/time tools

Calculation Method / Formula Explanation

Special cases (quick intuition)

Related Concepts / Background Info

Why max height depends on the vertical part

Mass doesn’t matter (in this model)

FAQs

How do I find the maximum height of a ball thrown up?

What angle has the longest flight time (ignoring air resistance)?

Does mass affect maximum height?

What factors affect projectile motion in real life?

Why does a higher angle usually increase max height?

What if I only know the max height — can I solve for launch speed?

Why is my measured maximum height lower than the calculator?

Is this calculator accurate for very long distances or bullets?

Limitations / Disclaimers

External References / Sources

Related Calculators

Trajectory Calculator

Free Fall Calculator

Free Fall with Air Resistance Calculator

Projectile Range Calculator

Projectile Motion Calculator

Time of Flight Calculator – Projectile Motion