Projectile Motion Calculator
Explore projectile range, height, and flight time
Compute trajectory outputs and velocity components with unit switching and LRU-style bidirectional solving.

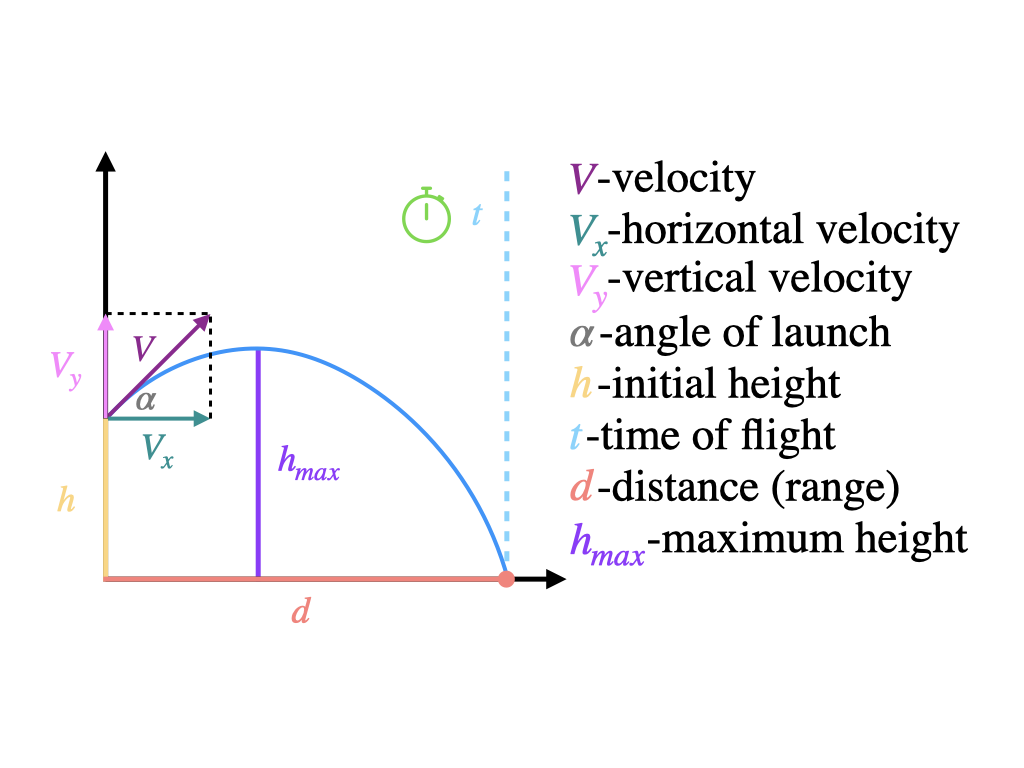
1) Introduction / Overview
This projectile motion calculator models the classic “parabolic flight” you see when you throw a ball, launch a water balloon, or shoot an arrow (ignoring air drag). It helps you connect what you can measure (like distance and time) to what you want to know (like launch speed, launch angle, peak height, and velocity components).
Who is this for?
Students (physics/homework), coaches (ball trajectories), makers (DIY launchers), and anyone doing a quick sanity check in engineering or simulation.
Why is it reliable?
It uses standard constant-acceleration equations with gravity, supports unit conversion, and can solve “forward” or “reverse” depending on which inputs you provide.
If you’re analyzing arrows, try the Arrow Speed Calculator. For pure vertical motion, the Free Fall Calculator is often a cleaner fit.
2) How to Use / Quick Start Guide
You only need three independent inputs for a full solution. Pick whichever three you actually know from your experiment. The calculator will fill the rest.
Enter what you know
Common combos: V + α + h (textbook), or t + d + hmax (measured flight).
Check the derived outputs
The calculator derives Vx, Vy, total flight time, range, and max height. If an output section is collapsed, it will highlight to tell you something changed.
Use “Flight parameters at given time” for snapshots
Set a time value and read the instantaneous velocity and height. It’s great for plotting or checking a mid-flight moment.
Example A: You know launch speed and angle
Suppose you throw a ball at V = 20 m/s, α = 35°, and from h = 1.5 m. Keep gravity at 9.81 m/s².
What you should notice
- Vx will be about 20 × cos(35°) ≈ 16.4 m/s.
- Vy will be about 20 × sin(35°) ≈ 11.5 m/s.
- The time of flight will be a bit longer than the “launch from ground” case because you start at 1.5 m above the landing level.
Example B: You measured distance and time
You record a launch that travels d = 30 m and lands after t = 2.0 s. The calculator can immediately infer Vx = d/t = 15 m/s (even before the full solve).
How to interpret the results
- Vx is constant (in this model), so it’s the cleanest measurement.
- If you also provide hmax or h, the calculator can recover the vertical side (Vy, α, and total V).
3) Real-World Examples / Use Cases
1) Sports throw (basketball / baseball)
Inputs: V, α, h.
Use: estimate whether the arc clears a defender and where it lands.
2) DIY launcher tuning
Inputs: d, t, hmax.
Use: back-calculate required launch speed and angle.
3) Arrow flight sanity check
Inputs: d and time from video frame count.
Use: estimate horizontal speed; then compare with the Arrow Speed Calculator.
4) Classroom lab: measure g (approx.)
Inputs: h, t (near-vertical) or y(t) points.
Use: check whether measured values are consistent with Earth gravity.
Practical note: if your projectile is light (ping-pong ball, paper, shuttlecock), air drag dominates and the real path won’t be a clean parabola. The calculator can still be a useful baseline — just don’t expect perfect agreement.
4) Common Scenarios / When to Use
Great fit when:
- You can reasonably ignore air resistance (dense/heavy projectile, short range).
- You want quick relationships between V, α, time, range, and peak height.
- You’re building intuition (how changing angle trades range vs. height).
Not a great fit when:
- Drag matters (very fast bullets, very light balls, long-range trajectories).
- You need wind, lift, or powered flight (drones, rockets, gliders).
Want a more aerodynamic view? The Ballistic Coefficient Calculator is a good companion when drag is part of the discussion.
5) Tips & Best Practices
Tip 1: Use time + distance for clean Vx
If you have video footage, counting frames is often the easiest way to estimate flight time. Then Vx = d/t is a strong anchor.
Tip 2: Sanity-check units first
Big mistakes usually come from mixing meters/feet or seconds/minutes. If the outputs look “wild,” double-check units before changing inputs.
Tip 3: Negative initial height is a clue
In reverse-solving modes (like t + d + hmax), a negative computed h usually means your measured constraints imply the projectile would need to start below the chosen “ground” level.
Tip 4: Use 45° as a baseline
With equal launch/landing height and no drag, 45° maximizes range. If your best range happens far from 45°, drag or measurement error may be involved.
6) Calculation Method / Formula Explanation
The calculator assumes constant gravity g and no air resistance. Horizontal acceleration is zero, and vertical acceleration is −g.
Velocity components
Vx = V · cos(α)
Vy0 = V · sin(α)
Position over time
x(t) = Vx · t
y(t) = h + Vy0 · t − (g · t²)/2
Key derived quantities
- Time of flight: solve y(t) = 0 for t > 0.
- Range: R = Vx · t_flight.
- Max height: h_max = h + Vy0²/(2g).
If you provide measurements like t and d, it can infer Vx immediately. Add a vertical constraint (like h or hmax) and the calculator can recover the vertical component and then the full V and α.
7) Related Concepts / Background Info
Projectile
In basic physics, a projectile is an object moving under gravity alone (no thrust). That’s why the math is so clean.
Why the path is a parabola
Horizontal motion is linear in time; vertical motion is quadratic in time. Combine them and you get a parabolic trajectory. If you want the pure math view, try the Parabola Calculator.
Fun intuition: a satellite is basically a projectile that’s moving so fast horizontally that the ground “falls away” beneath it.
8) Frequently Asked Questions (FAQs)
Does projectile motion have to move horizontally?
No. A straight-up toss is still projectile motion (horizontal component is zero). The defining feature is that gravity is the only acceleration.
Why does the horizontal velocity stay constant?
In this model, there’s no horizontal force. No horizontal force means no horizontal acceleration, so horizontal velocity stays the same.
What makes the trajectory a parabola?
Because x grows linearly with time while y includes a t² term. Eliminating time between them produces a quadratic relationship (a parabola).
Why is 45° often called “optimal”?
If launch and landing heights are equal and drag is negligible, the range is maximized near 45°. In real life (drag, wind, different heights), the best angle can shift.
Why did the calculator show a negative initial height?
That usually happens when you give constraints like t and hmax that imply the projectile would need to start below your chosen “ground” level to satisfy them. It’s not a software bug — it’s a clue about your assumptions or measurements.
Can I use this for bullets or long-range ballistics?
You can use it for a quick baseline, but real ballistics is drag-dominated. If you want to reason about drag, start with the Ballistic Coefficient Calculator.
9) Limitations / Disclaimers
This calculator is a physics model, not a promise. It assumes constant gravity and neglects air resistance, wind, lift, and spin.
- Results are most accurate for short-to-moderate ranges and dense projectiles.
- If you’re using measured data (video, sensors), small timing errors can cause noticeable differences in inferred angles or speeds.
- For safety-critical work (weapons, industrial systems), consult a qualified professional and validated simulation tools.
10) External References / Sources
- Galilei, G. (1638). Two New Sciences. Leiden. p. 249.
- Stewart, J., Clegg, D., & Watson, S. (2021). Calculus: Early Transcendentals (9th ed.). Cengage. p. 919. ISBN 978-1-337-61392-7.
- Tatum. (2019). Classical Mechanics (Chapter 7) [PDF].
- Thornton, S. T., & Marion, J. B. (2007). Classical Dynamics of Particles and Systems. Brooks/Cole. p. 59. ISBN 978-0-495-55610-7.
These references cover the core, no-drag projectile model used by this calculator (constant gravity, no air resistance). If you need wind/drag/lift, you’ll want a more advanced dynamics or ballistics model.
Related Calculators
Trajectory Calculator
Have a look at the flight path of the object with this trajectory calculator.
Free Fall Calculator
Calculate free fall parameters including gravitational acceleration, drop height, fall duration, and impact velocity. Supports bidirectional LRU solving with unit conversions.
Free Fall with Air Resistance Calculator
Calculate free fall with quadratic air drag, including terminal velocity, fall time, maximum velocity, and drag force. Supports air resistance coefficient calculation from object properties.
Projectile Range Calculator
Calculate the horizontal range of a projectile based on velocity, angle, and initial height. Supports bidirectional calculation with multiple unit systems.
Maximum Height Calculator – Projectile Motion
Use this maximum height calculator to figure out what is the maximum vertical position of an object in projectile motion.
Time of Flight Calculator – Projectile Motion
Check out how long a projectile remains in the air with this time of flight calculator.